This is a deconstuction of matematikaadit’s submission to therubygame challenge 5; ‘Roman numerals. What are they good IV?’. The goal of the challenge is to take a string representing a roman numeral as input and return the integer that the numeral represents.

matematikaadit currently has the honour of the shortest (by character count) submission for this challenge. At first glance I didn’t understand how it worked so I re-wrote and analyzed it until I did.

Making it readable

matematikaadit’s original submission:

def to_arabic_numeral(roman)
  n=s=0;roman.bytes{|c|s+=n-2*n%n=10**(205558%c%7)%9995};s+n
end

That’s pretty unreadable to me. Lets apply some formatting:

def to_arabic_numeral(roman)
  n = s = 0
  roman.bytes { |c|
    s += n - 2 * n % n = 10 ** (205558 % c % 7) % 9995
  }
  s + n
end

and some bracketing:

def to_arabic_numeral(roman)
  n = s = 0
  roman.bytes { |c|
    s += n - ((2 * n) % (n = ((10 ** (205558 % c % 7)) % 9995)))
  }
  s + n
end

and introduce some variables:

def to_arabic_numeral(roman)
  n = s = 0
  roman.bytes { |c|
    last_n = n
    n = (10 ** (205558 % c % 7)) % 9995 
    i = last_n - ((2 * last_n) % n)
    s += i
  };
  s + n
end

and some better named variables:

def to_arabic_numeral(roman)
  value = sum = 0
  roman.bytes { |char_code|
    last_value = value
    value = (10 ** (205558 % char_code % 7)) % 9995 
    increment = last_value - ((2 * last_value) % value)
    sum += increment
  }
  sum + value
end

and lastly add some logging:

def to_arabic_numeral(roman)
  value = sum = 0
  roman.bytes { |char_code|
    last_value = value
    value = (10 ** (205558 % char_code % 7)) % 9995 
    increment = last_value - ((2 * last_value) % value)
    sum += increment
  
    puts [
           "char:#{char_code.chr}",
           "char_code:#{char_code}",
           "value:#{value.to_s.ljust(4)}",
           "last_value:#{last_value.to_s.ljust(4)}",
           "increment:#{increment.to_s.ljust(4)}",
           "sum:#{sum}"
         ].join('  ')
  }
  sum + value
end

to_arabic_numeral('MCMXCIX') #=> 1999

When run this prints:

char:M  char_code:77  value:1000  last_value:0     increment:0     sum:0
char:C  char_code:67  value:100   last_value:1000  increment:1000  sum:1000
char:M  char_code:77  value:1000  last_value:100   increment:-100  sum:900
char:X  char_code:88  value:10    last_value:1000  increment:1000  sum:1900
char:C  char_code:67  value:100   last_value:10    increment:-10   sum:1890
char:I  char_code:73  value:1     last_value:100   increment:100   sum:1990
char:X  char_code:88  value:10    last_value:1     increment:-1    sum:1989

We see that the sum is always one iteration behind and the last value is added to sum after the loop is finished.

There’s two separate complicated lines here; the conversion of char_code into value and the calculation of increment.

Converting from numeral to integer

First lets look at the calculation of value which converts the ascii character code of a numeral to the integer the numeral represents:

 
value = (10 ** (205558 % char_code % 7)) % 9995 

Lets wrap the to a function that takes a character:

def roman_numeral_to_integer(char)
  char_code = char.ord
  (10 ** ((205558 % char_code) % 7)) % 9995
end

remind ourselves of the expected mappings: I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000

and see if it works:

roman_numeral_to_integer('I') # => 1
roman_numeral_to_integer('C') # => 100

roman_numeral_to_integer('i') # => 1000
roman_numeral_to_integer('Z') # => 5

It appears to work fine for any of the roman numerals and is undefined for other characters. Lets plug some more values into it:

numerals = "IVXLCDM"
('A'..'Z').each { |c| 
  value = roman_numeral_to_integer(c)
  puts "char:#{c} value:#{value.to_s.ljust(4)}  #{'*NUMERAL*' if numerals.include?(c) }"
}

Which prints:

char:A  value:1     
char:B  value:500   
char:C  value:100   *NUMERAL*
char:D  value:500   *NUMERAL*
char:E  value:1     
char:F  value:1000  
char:G  value:500   
char:H  value:1     
char:I  value:1     *NUMERAL*
char:J  value:5     
char:K  value:100   
char:L  value:50    *NUMERAL*
char:M  value:1000  *NUMERAL*
char:N  value:1     
char:O  value:1     
char:P  value:1000  
char:Q  value:50    
char:R  value:1000  
char:S  value:10    
char:T  value:1000  
char:U  value:1     
char:V  value:5     *NUMERAL*
char:W  value:10    
char:X  value:10    *NUMERAL*
char:Y  value:10    
char:Z  value:5

There’s no simple pattern to exploit in the relationship between ascii character codes and the distribution or magnitude of roman numerals.

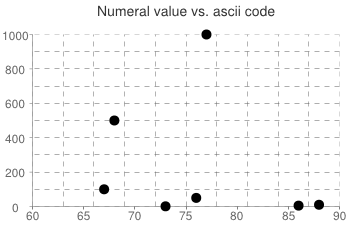
Instead roman_numeral_to_integer is a cleverly constructed function that fits all the points on the above graph, mapping all the roman numerals to integers. A lookup hash is certainly more easily constructed, read, and maintainable but this wins on cleverness and character count.

For more about a similar ‘Magic Formula’ for the same purpose, and how you could construct it using brute force methods see Golf: Magic Formula for Roman Numerals.

If you want to play around with this function try Wolfram Alpha: plot (10 ^ ((205558 mod floor(x)) mod 7)) mod 9995, x=65 to 90

Calculating the increment

Now lets look at increment. Increment is the value that should be added to sum. Because the sum calculation is one iteration behind it is last_value and not value that should be added.

increment = last_value - ((2 * last_value) % value)

When a smaller numeral is before a larger one it should be subtracted rather than added to the total so the increment will be -last_value when last_value < value, and else will just be last_value

The code works because, for the natural numbers x and y:

x % y ≡ x, when x < y 
x % y ≡ 0, when x >= y and y is a factor of x

Note that for any numeral value x all smaller numeral values are factors. For example, L (50) is greater than I (1), V (5), X (10) and all of these are factors.

So when last_value >= value it just added to sum (the right hand side of the subtraction will be 0) and when last_value < value it is turned negative (the right hand side of the subtraction will be last_value * 2).

Going back to the original program it looks like we only save 1 character doing it this way over a ternary if:

l-2*l%n
# vs.
n>l?-l:l

But remember that in the original program last_value and value are both stored in the single variable n. The program relies on the order of evaluation to use the correct value of n whereas a ternary if will evaluate the conditional first so would require a new variable to be used.

Summing up

The method has clever use of a mathematical function for mapping numerals and modulus operation to avoid an if statement. Most of this is done in a single expression and trusts the evaluation order semantics of Ruby.